Why Compounding Doesn’t Work the Way You Think It Does!
What the Investment Media Is Lying to You About
Most of the readers of this blog will be aware of the power of compound interest. It’s often referred to as “ the eighth wonder of the world. He who understands it, earns it … he who doesn't … pays it.” (allegedly a quote from Albert Einstein)
There is no lack of inspiring quotes from the world’s greatest investors on this subject. Here’s one of my most favorite ones from the GOAT Warren Buffett himself:
“It is obvious that a variation of merely a few percentage points has an enormous effect on the success of a compounding (investment) program. It is also obvious that this effect mushrooms as the period lengthens. If over a meaningful period of time, Buffett Partnership can achieve an edge of even a modest number of percentage points over the major investment media, its function will be fulfilled.” - Warren Buffett
I'm sure you've come across statistics and investing-related news article headlines that begin like this:
"If you had invested $10,000 in [asset / stock / ETF] [x] years ago, here's how much money you would have ..."
If you invested $10,000 in the S&P 500 in Jan 2003, it would have grown to $64,844 by Dec 2022 (+548% return)
If you'd invested $10,000 in Alphabet ten years ago, you'd now own $49,000 worth of Google stock.
If you'd invested $10,000 in Apple when Warren Buffett first bought it, and didn't sell any shares along the way, your investment would be worth nearly $66,000 today.
In the real world, however, compounding is not as powerful as you might think - because of four factors!
It seems to me that these four factors are often overlooked, so today I want to shed some light on why compounding doesn't work the way you think it does…
Assumptions
Let's start with some basic assumptions. We're looking at a young investor, Charlotte, who starts with no initial capital. However, she will invest $1,000/month ($12,000 per year) for 30 years. She earns a compounded annual return of 10% over this period.
After 30 years, Charlotte's net worth will have grown to $2,080,849,39!
Not bad for someone on a basic salary who just early on made the decision to consistently put some of her savings into the stock market.
But let's discuss why Charlotte's ACTUAL final net worth will be lower than the number above!
Factor #1: Fees
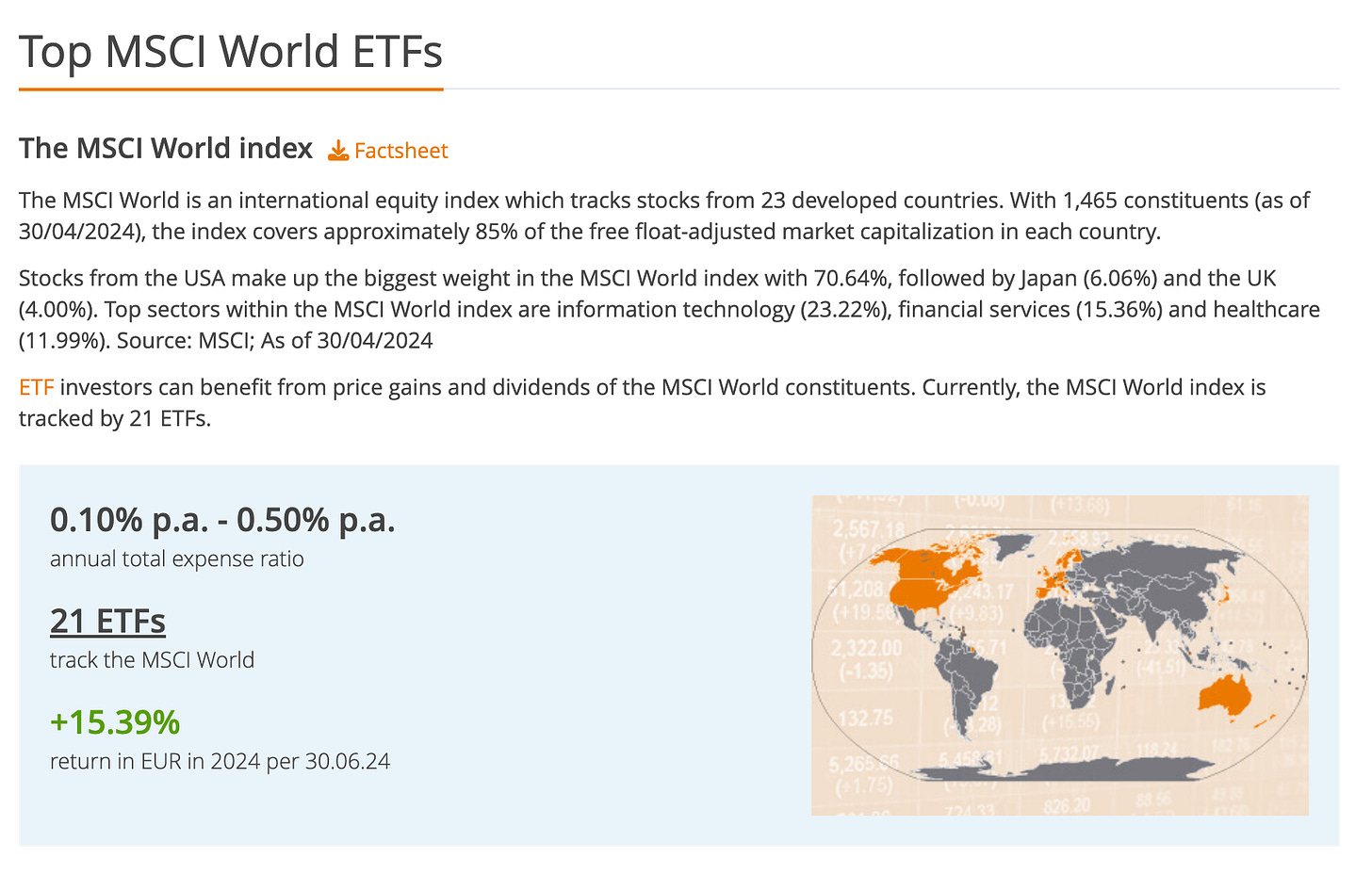
Let's say Charlotte invests in 1-2 ETFs. Of course, as an investment product, ETFs are unrivaled in terms of the fees that investors have to pay.
The amount of fees that investors have to pay varies considerably from one investment product to another though.
I just looked at JustETF – an ETF comparison website – and apparently the fees charged for MSCI World ETFs vary from 0.1-0.5%.
Let's take 0.2% per annum and do the compounding again (that 0.2% per annum is just gone!). Instead of around $2.08 million, she ends up with $80,000 less! (the final net worth is displayed in the bottom right corner of the chart below)
Of course, fees vary from product to product! I'm aware that there are ETFs that charge less than 0.1% p.a., but regardless of what the actual fees are, it's important to understand that they have an impact on investors’ real returns.
Factor #2: Taxes
The second variable to consider is the impact of taxes - and specifically capital gains tax rates.
Capital gains tax rates vary widely between countries, and sometimes even between states within a country.
But many people who save diligently and invest successfully for decades, like Charlotte, will eventually be “penalized” by having to pay capital gains tax.
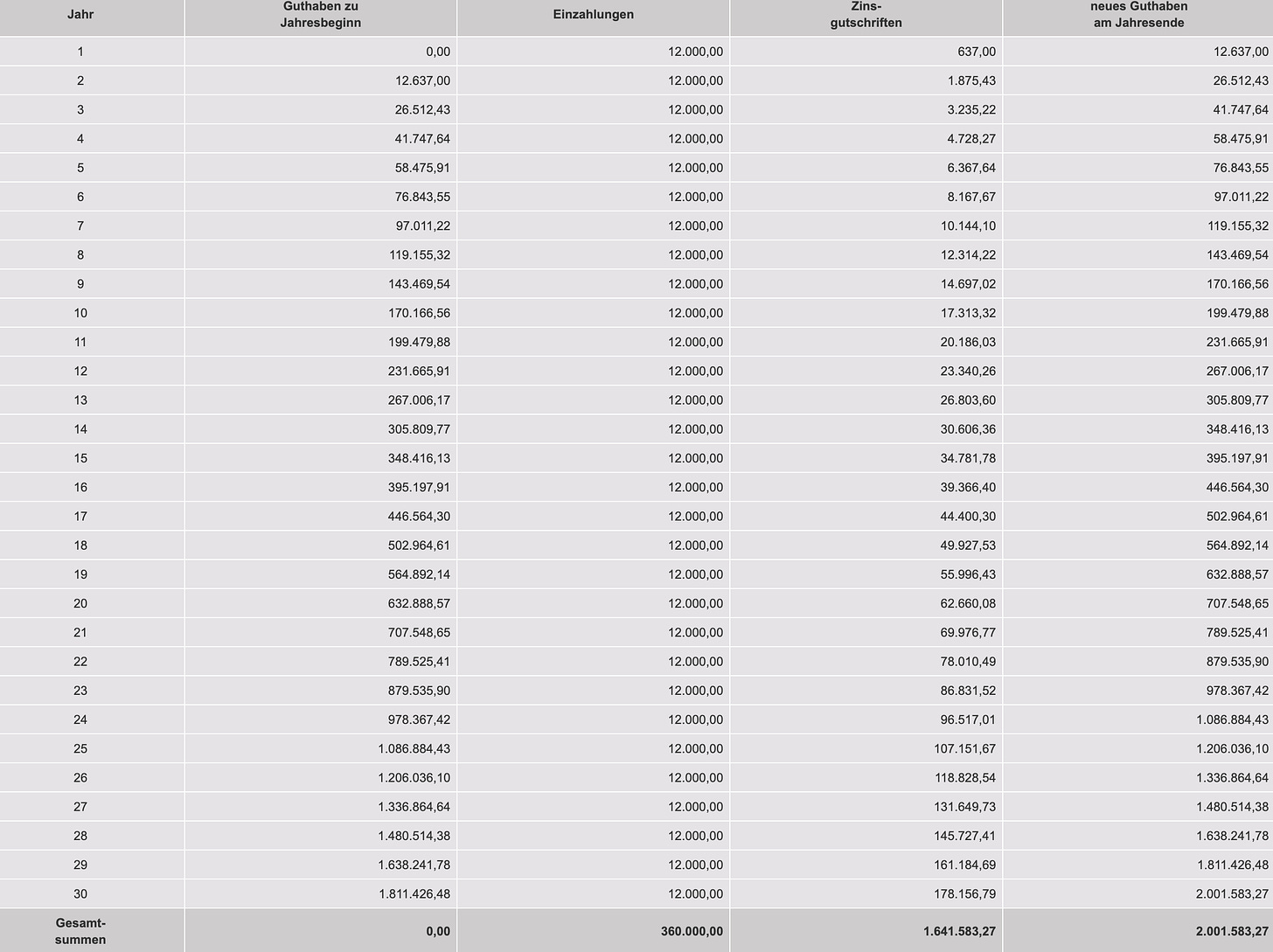
Of the $2,001,583 that Charlotte ended up with after compounding at 9.8% for 30 years, she contributed $360,000 in savings, which means that $1,641,583 of the $2 million are capital gains.
I'll try to keep the maths simple here. Let’s assume Charlotte lives in Germany. In Germany, as of 2024, the capital gains tax rate is 26.357%.
This means that if Charlotte sells her ETFs at the start of her retirement, she'd have to pay $432,967 in capital gains tax ($1,641,583*0.26357), leaving her with $1,568,616 ($2,001,583-$432,967).
The critical reader will point out that this example is perhaps a little too simplistic. And you are right!
First and foremost, Charlotte would probably not sell her entire ETF portfolio after 30 years, but rather sell a small portion of it periodically to cover her living expenses. The rest would remain invested and hopefully continue to compound for a long time (or, if her withdrawal rate is low enough, forever!).
Also, under German tax law, equity ETFs in particular are partially exempt from capital gains tax (30% partial exemption).
But if you're going to get into the details of German tax law, you'll also have to point out that there's a fairly new rule that hinders the compounding process. The so-called "Vorabpauschale" is an upfront tax payment on potential gains from accumulating ETFs.
In addition, critical readers will point out that no one knows how capital gains will be taxed in the future - whether the capital gains tax rate will be higher or lower, whether tax-free retirement accounts will be introduced or not, etc.
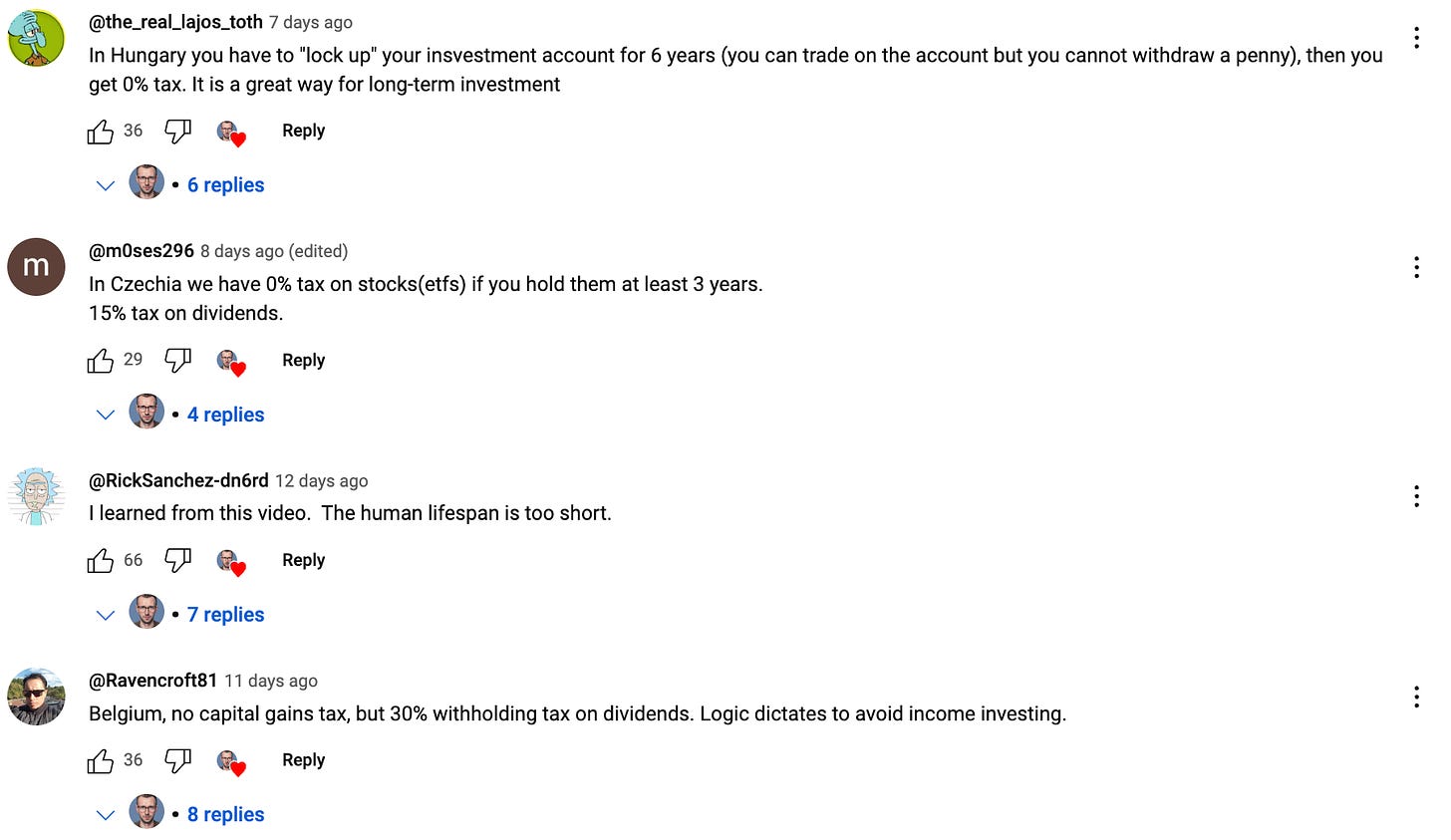
After I released my YouTube video on this topic, hundreds of viewers shared the capital gains tax rates in their respective countries. It was amazing to see how different tax systems can be! Some countries have managed to set up a system that really incentivizes long-term investment by charging lower or no capital gains tax after certain holding periods.
How much capital gains tax do you have to pay?
Factor #3: Inflation
The third factor that few people mention when discussing the power of compounding is the effect of inflation.
The REAL return on an investment is the annual percentage return on an investment adjusted for inflation or other external factors. This adjustment provides a clearer picture of the real purchasing power gained (or lost) from an investment over a given period of time.
We all know that central banks have only recently succeeded in reducing inflation rates. But even assuming a modest 2% annual currency depreciation, Charlotte's real purchasing power after 30 years will be significantly less than the original calculated figure might suggest.
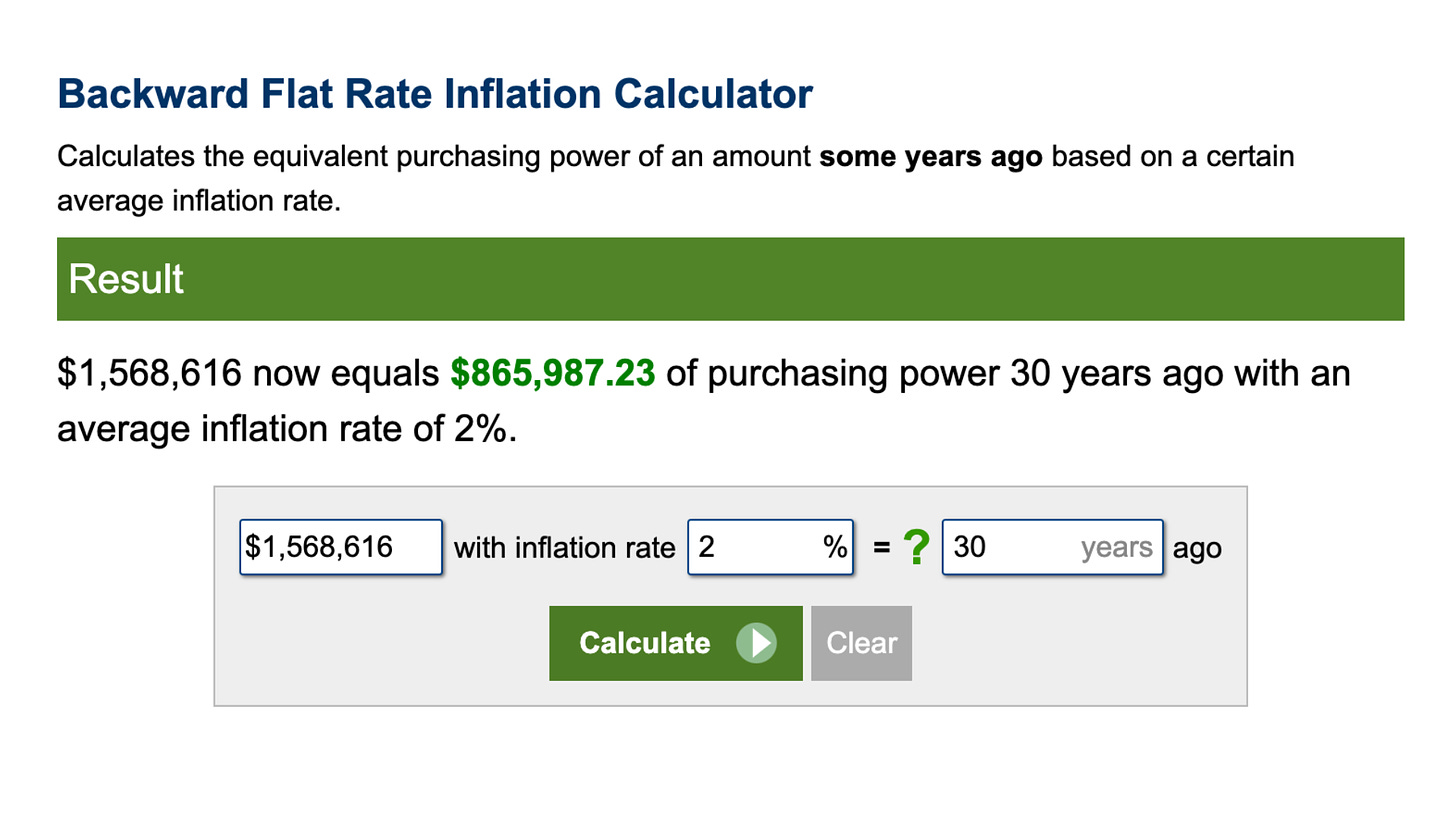
I've found this great inflation calculator site that allows you to work out your future purchasing power. Assuming an average inflation rate of 2% over the 30-year period, Charlotte's $1,568,616 will only have the purchasing power of $865,987 today.
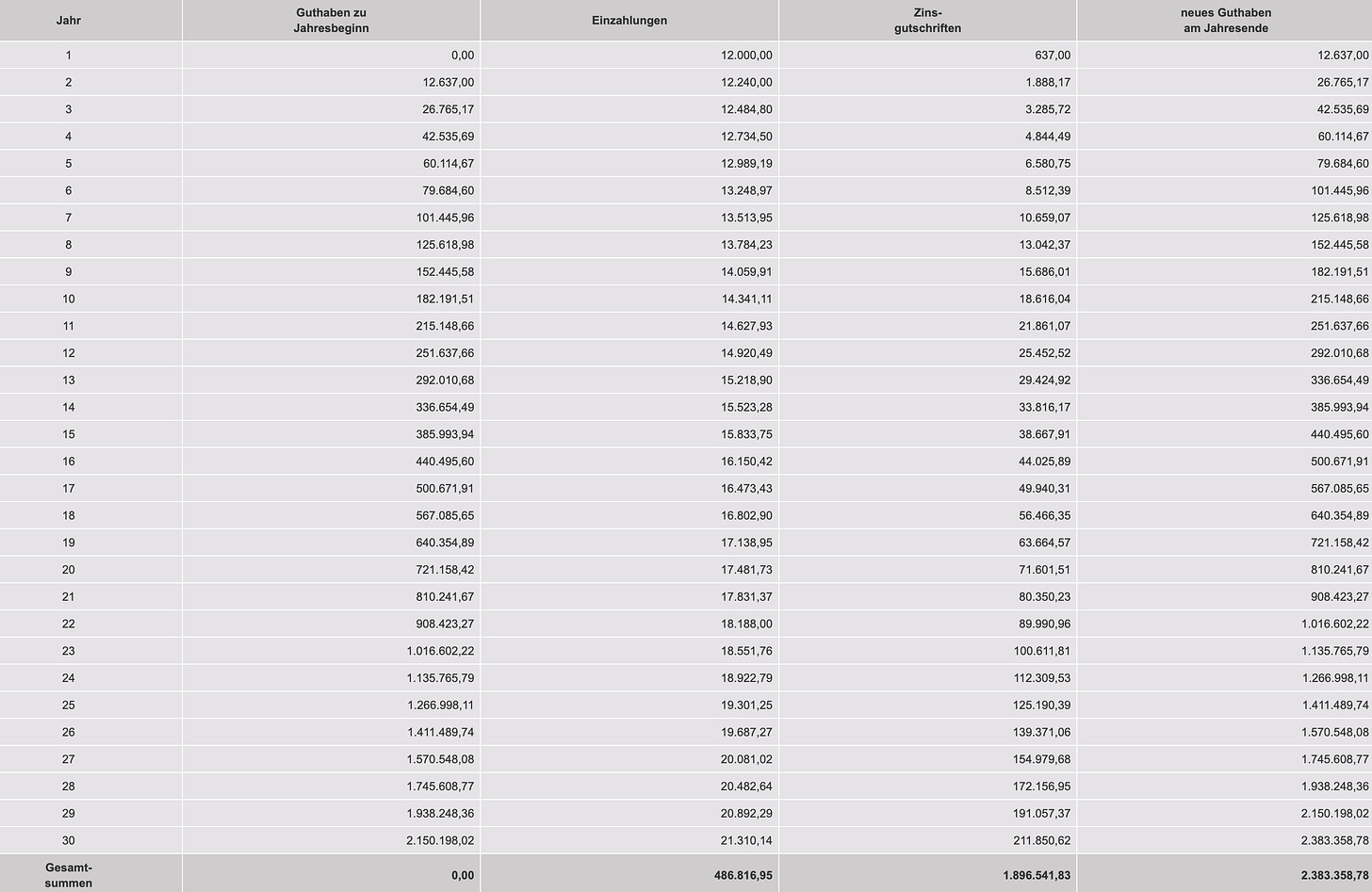
So to protect against the world's cruelest tax (aka inflation), investors need to INCREASE their savings rate by at least the rate of inflation.
If Charlotte were to increase her monthly contributions by 2% a year, she'd end up with $2,383,358.78 before tax, assuming a CAGR of 9.8%.
Of course, if you can increase your savings rate faster than the rate of inflation, you will do even better.
Factor #4: Sequence of Return Risk
In investing, it is not only the future return that is uncertain, but also the order in which the annual returns will occur.
The so-called “sequence of return risk” refers to the potential negative impact on an investment portfolio’s value caused by the order in which investment returns occur. This risk becomes crucial when an investor is regularly withdrawing money, such as during retirement, or making periodic contributions to the portfolio – if an investor does not withdraw or contribute money during the investment period, the sequence of returns is irrelevant.
However, when withdrawals or contributions are involved, the sequence of returns becomes highly significant. For retirees making regular withdrawals, experiencing poor returns early in retirement can be particularly detrimental. These early losses can deplete the portfolio more quickly, leaving less capital to benefit from potential future gains. Conversely, experiencing good returns early in retirement can help sustain withdrawals and reduce the risk of running out of money, as the portfolio grows more robustly from the outset.
The same principle applies to investors making regular contributions – like Charlotte in our example. Poor returns early in the investment period mean buying more shares when prices are low, potentially leading to greater gains when the market recovers. On the other hand, good returns early on result in purchasing fewer shares as prices are higher and future expected returns lower, which will lead to lower overall absolute gains.
The calculations above assumed a steady return of 10% annually which one will not witness in the real world. Hence, Charlotte will likely end up with a lot more or less after 30 years depending on the sequence of the returns.
What's the Point of This Post?
The message I want to get across with this article is NOT that using compounding calculators is pointless! No, quite the opposite! I think compounding calculators can be incredibly powerful, an eye-opener for people new to investing, and a great source of motivation to get started and delay gratification.
Getting started is perhaps the most important step any investor takes on their journey to financial independence - the sooner you start the better!
Keep going and try not to interrupt the power of compounding.